中考数学开放型附加模拟试题

【摘要】中考即将来临，在考试后，不管考得好与不好，大家一定都有一些反思和感想。小编为大家整理了中考数学附加题，供大家参考。

开放型试题重在开发思维，促进创新，提高数学素养，所以是近几年中考试题的热点考题。观察、实验、猜想、论证是科学思维方法，是新课标思维能力新添的内容，学习中应重视并应用。

例1．(2005年梅州)如图，四边形ABCD是矩形，O是它的中心，E、F是对角线AC上的点。

(1)如果           ，则ΔDEC≌ΔBFA(请你填上能使结论成立的一个条件);

(2)证明你的结论。

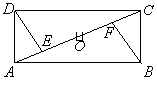
分析：这是一道探索条件、补充条件的开放型试题，解决这类问题的方法是假设结论成立，逐步探索其成立的条件。

解：(1)AE=CF(OE=OF;DE⊥AC;BF⊥AC;DE∥BF等等)

(2)∵四边形ABCD是矩形，∴AB=CD，AB∥CD，∠DCE=∠BAF

又∵AE=CF，∴AC-AE=AC-CF，∴AF=CE，∴ΔDEC≌ΔBAF

说明:考查了矩形的性质及三角形全等的判定。

练习一

1. (2005年黑龙江课改)如图, E、F是□ABCD对角线BD上的两点，请你添加一个适当的条件: ___________ ，使四边形AECF是平行四边形.

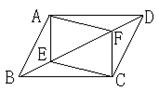
2、(2005年金华)如图，在△ABC中，点D在AB上，点E在BC上，BD=BE.

(1)请你再添加一个条件，使得△BEA≌△BDC，并给出证明.

你添加的条件是：    .

证明：

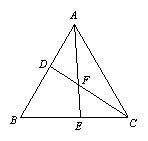
(2)根据你添加的条件，再写出图中的一对全等三角形：    . (只要求写出一对全等三角形，不再添加其他线段，不再标注或使用其他字母，不必写出证明过程)

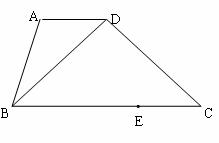
3、(2005年玉溪)如图，在梯形ABCD中，AD∥BC，BD=CD，AB

问：当CE分别为何值时，四边形ABED是等腰梯形?直角梯形?请分别说明理由。

练习二

1、(2005年武汉)如图1，AB是⊙O的直径，AC是弦，直线EF和⊙O相切于点C，AD⊥EF，垂足为D。

(1)求证：∠DAC=∠BAC;

(2)若把直线EF向上平行移动，如图2，EF交⊙O于G、C两点，若题中的其他条件不变，这时与∠DAC相等的角是哪一个?为什么?

2. (2005年包头) 如图1，⊙O1与⊙O2都经过A、B两点，经过点A的直线CD与⊙O1交于点C，与⊙O2交于点D。经过点B的直线EF与⊙O1交于点E，与⊙O2交于点F。

(1)求证：CE∥DF;

(2)在图1中，若CD和EF可以分别绕点A和点B转动，当点C与点E重合时(如图2)，过点E作直线MN∥DF，试判断直线MN与⊙O1的位置关系，并证明你的结论。

3、(2005年四川)己知：如图，E、F分别是□ABCD的AD、BC边上的点，且AE=CF。

(1)求证：△ABE≌△CDF;

(2)若M、N分别是BE、DF的中点，连结MF、EN，

试判断四边形MFNE是怎样的四边形，并证明你的结论。

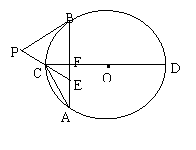
4、(2005年黄冈)如图，已知⊙O的弦AB垂直于直径CD，垂足为F，点E在AB上，且EA = EC。

⑴ 求证：AC2= AE·AB;

⑵ 延长EC到点P，连结PB，若PB = PE，试判断PB与⊙O的位置关系，并说明理由。

5、(2005年枣庄)如图，⊙O1和⊙O2外切于点P，直线AB是两圆的外公切线，A,B为切点，试判断以线段AB为直径的圆与直线O1O2的位置关系，并说明理由.

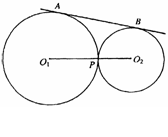
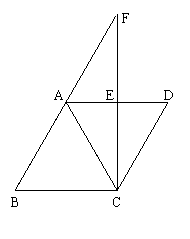
例2、(2005年陕西课改)如图，直线CF垂直且平分AD于点E，四边形ADCB是菱形，BA的延长线交CF于点F，连接AC。

(1)       图中有几对全等三角形，请把它们都写出来;

(2)证明：△ABC是正三角形。

分析：本题需学生根据给定的条件，通过观察，分析，探索多个不明确的结论。求解此类问题时，切勿凭空乱想，应仔细对照条件，观察图形特征，联想已学知识，方法或已解决过的问题，全方位的、多角度地作全面分析。

解：(1)图中有四对全等三角形，分别为△ABC≌△CDA，△AEF≌△DEC，△DEC≌△AEC，△AEF≌△AEC。

(2)证明：

∵CF垂直平分AD，

∴AC=CD

又∵四边形ABCD是菱形，

∴AB=BC=CD=DA

∴AB=BC=AC

∴△ABC为正三角形。

[1] [2]  下一页