一道值得研究的思考题

　　　　作为一名数学教师，总有美好的期待，希望能用数学内在的魅力，深深地吸引学生去探索数学的奥秘，感受数学在生活中的广泛应用，从而投身于数学研究。今年四月份，全国著名特级教师刘德武老师在宁波推出最新的观摩课——“卫生纸的长度”。在课上刘老师用他精湛的教学技艺引导学生积极参与“做数学”的过程，探索卫生纸的厚度、圈数，并解决卫生纸的长度，他还特意花了二三分钟时间用米尺测量出这卷卫生纸的长度。最后，刘老师意味深长地问：“我们为什么要用整整一节课的时间去探索只需二三分钟就能解决的问题呢?而且得出的还是误差很大的结果。”其中一位学生动情地说：“我认为今天得到的结果并不重要，重要的是我们学会探究的方法，体验到了数学学习的价值……这节课我认为很有意义。”这一段精彩的对白在台下听课的老师中赢得了热烈的掌声，台上、台下产生了强烈的情感共鸣。
　　　　其实，数学的魅力就在于它具有诱人的美，而一道构思精巧的习题会让你回味无穷。刘德武老师的“卫生纸的长度”这节课，使我回想起第六届“华杯赛”复赛中一道耐人寻味的几何题。这道几何题原意是这样的：
　　　　下图是一卷紧紧缠绕在一起的牛皮纸，纸卷直径为20厘米，中间有一直径为8厘米的卷轴。已知纸的厚度为0．4厘米，试求这卷牛皮纸展开后大约有多长?(π=3．14)
　　　　
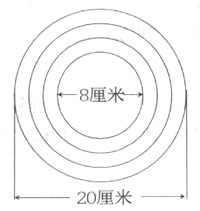
　　　　当时在数学活动课上向学生出示这道题目时，我预想得很简单，按照一般的“演绎”思路“按部就班”地进行讲解：这卷纸共有(20-8)÷2÷0．4=15(圈)，设这卷纸的总长为C厘米，每圈的长度分别为C₁、C₂、C₃……C₁₅₀
　　　　C₁≈π×(8+O．4×2)
　　　　C₂≈π×(8+0．4×4)
　　　　C₁₅≈πx(8+O．4×30)
　　　　C≈π×[8×15+0．4×(2+4+6+……+30)]
　　　　=216π
　　　　=678．24(厘米)
　　　　算到这里，该题已经解决了。没有想到旁边的一位学生提出异议：“老师，我觉得每圈牛皮纸的长度不应该这样算。我觉得……”他边说边拿起讲台上的粉笔在黑板上画圈，即◎。他接着解释道：“每圈牛皮纸展开后的长度应比外圈的周长短，比内圈的周长长一些，取中间这部分(指着虚线)的长度才合理呀。”真有见解!我不由得鼓掌表扬他爱动脑筋，并接着问：“如果按你的想法，这道题该怎样计算呢?”他自信地拿起粉笔在我原来的算式上改动起来。
　　　　C₁≈π×(8+0．4×1)
　　　　C₂≈π×(8+0．4×3)
　　　　……
　　　　C₁₅≈π×(8+O．4×29)
　　　　C≈π×[8×15+0．4×(1+3+5+……+29)]
　　　　=659．4(厘米)
　　　　“真聪明，每圈的直径都少1个0．4厘米。”也许正是这位学生的大胆质疑引起了其他学生的思考，教室里顿时鸦雀无声。这时，另一位学生举手发言：“老师．这样做是否太麻烦?我认为求15圈牛皮纸的总长度，不如先求出这15圈的平均长度，再乘以15。”我听了不禁一愣。对呀!这15圈的长度其实就是等差数列，用中间数求和，是再方便不过了。
　　　　“你有什么高明的方法解决这15圈牛皮纸的平均数呢?”我反将他一军。
　　　　他想了想说：“这卷牛皮纸共有15圈，第8圈的长度就是它们的平均数。”边说边神气地在黑板上演算起来。
　　　　3．14×(8+O．4×15)＝43．96(厘米)
　　　　43．96×15=659．4(厘米)
　　　　厉害!我差点喊出声来。此时，我真为我的学生感到骄傲。这道题就在我们师生互动中解决了。后来几天，我也没把这道题放在心上。一周过去了，上次第一次挑毛病的学生找到了我，悄悄地对我说：“老师，上次那道牛皮纸的题目，还有更简便的方法。”我一下子被他吊起了胃口：“真的吗?”他自信地点点头，于是他拿出纸慢慢地画了起来。他的大概意思就是将这卷纸全部展开后，它的正侧面可以近似地看作一个长方形。这个长方形的长就是这卷牛皮纸的长度，宽就是牛皮纸的厚度，所以长方形的面积应近似地等于原来这卷牛皮纸的侧面积(圈环的面积)。
　　　　纸的长度＝长方形的面积／长方形的宽
　　　　≈纸卷侧面积／纸的厚度
　　　　＝3.14×10²-3.14×4²／0.4
　　　　＝659.4(厘米)
　　　　一语激醒梦中人!本来看似一道普通的数学题目。经过“化曲为直”的转化后，变成一道求长方形长的题目，难度顿时化解，其道理与方法竟是如此的浅显。此题将圈环转化为近似长方形，这与课本中将圈环拉直为线段，将圆面割拼成近似长方形，将圆柱的侧面展开成长方形的数学思想，竟有如此多的异曲同工之处。而这“化曲为直”的转化思想正是我们探索曲线、曲面必备的数学思想与方法，我暗暗惊讶于学生丰富的想像力、敏锐的观察力和大胆的创造力。接下来的好长一段时间，我陷入了沉思之中。
　　　　回顾探索这卷牛皮纸长度所经历的过程，觉得此时。获得问题的结果对我们来说已不重要了，重要的是师生们在思维的碰撞中，不断丰富内心体验。不断积累数学感觉。作为一名数学教师，该拿什么奉献给我们的学生?一道充满灵性的数学题，不正如一把开启智慧之门的钥匙?让我们的学生在探索数学问题中，不断被数学的奥秘所吸引，不断获得成功的满足和精神的愉悦。我想，这应该是这道思考题留给我们的另外一个思考吧!