解决问题：点燃计算教学亮色

　　对于“计算教学”，新教材的编排体系发生了显著变化。它大胆打破了老教材的传统格局，把“计算教学”和“解决问题”有机整合，使得“计算教学”能依托“解决问题”，凸显计算意义，丰富计算策略，落实计算素养。这样的创新编排，给“计算教学”走出低谷、迈向高效预设了广阔的实践空间，从而激励着诸多有识之士为此探索不止、实践不息。走进浙江省著名特级教师汪培新老师执教的“中括号”课堂现场，我们可以欣喜地发现：“计算教学”与“解决问题”的整合形态，已超越了“简单叠加”的肤浅层面，达到了“无逢对接”的成熟境界。在此，笔者仅摘录该课教学的三个片断，与同行共读、共赏、共思。
　　片断一：自主提问，营造“中括号”的产生背景
　　师：老师这里有一组信息(屏幕出示以下内容)，根据这组信息，你们能提出什么数学问题?
　　300元钱，买12个网球后还剩60元。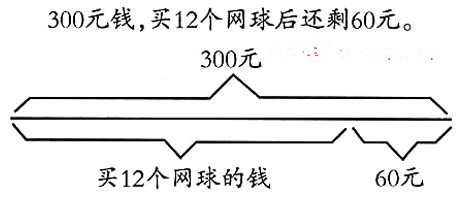
 
　　生1：剩下的钱还可以买几个网球?(板书：剩下的钱可买几个这样的网球?)
　　生2：每个网球的单价是多少元?
　　师：这个问题你们会求吗?怎么求?
　　生3：60÷12=5(元)。
　　师：每个网球5元，有问题吗?
　　生4：应该是(300-60)÷12=20(元)。
　　师：是的。从图中很容易看出，12个网球对应的钱是300元减60元的差，所以(300-60)÷12才能算出网球的单价。(对生3)明白了吗?
　　生3：明白了，刚才看错了!
　　生5：如果300元钱都买网球，能买多少个?(板书：300元钱可买几个这样的网球?)
　　生6：要买20个网球，300元钱够吗?
　　师：这也是求“买几个网球需要多少钱”的问题。为了方便研究，我们可以把这个问题简化一下。(板书：买5个这样的网球要多少钱?)
　　教学伊始，汪老师提供了一组精心设计且图文并茂的素材信息，引导学生展开提问。我们看到，在这个过程中，学生先后提出了两类数学问题：一类是需要两步计算解决的数学问题(不需要用中括号)，如“每个网球的单价是多少元”等。这类问题对“中括号”教学而言，属于前位旧知层面。对此，汪老师让学生当场口头解决，这样既复习了两步计算应用题的数量关系，又回忆了两步计算式题的书写格式。另一类是需要三步计算解决的数学问题(需要用到中括号)，如“剩下的钱可买几个这样的网球”、“300元钱可买几个这样的网球”、“买5个这样的网球要多少钱”等。这类问题的后续解答，将会促成“中括号”的应需而生，所以说，这类问题是新课教学的重要凭借。因此，汪老师极其认真地将这类问题板书于黑板上，并不时地对学生问题表达的科学性予以指正。我们可以看到，在学生整个“自主提问”的过程中，汪老师既适度关注了计算教学的必要铺垫，同时又巧妙营造了新知生成的背景平台。
　　片断二：尝试解答，揭示“中括号”的价值内涵
　　师：同学们已经提出了很多数学问题，那么，这些问题你们自己能解决吗?因为有好几个问题，所以请大家首先解决“剩下的钱可买几个这样的网球”这个问题。
　　(学生开始尝试解决，教师来回巡视。两分钟后，交流开始)
　　生1：我先求出每个网球的单价(300-60)÷12=20(元)，然后再计算60÷20=3(个)。(板书算法)
　　生2：我的方法是60除以……我用了一个中括号。
　　师：哦！你是直接列成了一个算式，拿上来给大家看看。
　　生2(展示解法)：(300-60)÷12算的是网球的单价，再除60就可求出剩下的钱能买几个网球了。(算式如下)
　　60÷［(300-60)÷12］
　　=60÷(240÷12)
　　=60÷20
　　=3(个)
　　师：其他同学看懂他的方法没有?(学生大都表示看得懂)有多少同学也是用这种方法解决问题的?(近十位学生举手)真了不起!那么，这种方法中用到的“［］”符号，大家知道是什么符号吗?
　　生：中括号!
　　师：为什么在这个算式中，要使用中括号呢?
　　生2：如果不用中括号，那算出的得数就不一样了。
　　师：什么意思?能说得具体一些吗?
　　

　 www.xiaozhibei.com 生2：不用中括号的话，第二步就要算60÷240了。
　　师：而我们先要算的是240÷12，所以要加上中括号!看来，中括号的作用是为了使某些步骤可以先算。对于这种方法，你们还有什么问题吗？
　　生3：我觉得运算的时候有点问题。第一步240÷12的外面不应该是小括号，应该是中括号。
　　生4：我有意见!中括号里面的300-60已经算出来了，所以中括号要变成小括号。
　　生5：因为中括号里的小括号已经算出来是240，所以原先的小括号没有了，而原先的中括号要抄下来。
　　师：大家看，这个240÷12是原来算式中小括号里的内容，还是中括号里的内容?
　　生：中括号!
　　师：所以，为了看得更清楚一些，我们在脱式计算时，仍旧要把没有轮到计算的中括号抄下来，而不改成小括号。明白了吗？还要注意的是，脱式计算时等号要对齐，既整洁美观，又方便检查。
　　生6：我还有一种方法，是300÷［(300-60)÷12］-12……
　　翻看教材，可以发现，本课学习之前学生已经广泛接触了此类应用问题的探究解决。换而言之，绝大部分学生都能凭借自身已有的学习经验，独立解答先前提出的三步计算数学问题。所不同的是，多数学生会采用“分步列式”的方法进行解答，因为这种方法符合以前解决此类问题的格式规范。但也有少数学生则立足更高的学习起点，直接采用“综合列式”的方法进行解答，使得“中括号”由此呈现。当然，此时的“中括号”只是少数学生的“局部性”产物，还没有成为全体学生的“全局性”成果。因此，如何促成“中括号”的认识由“局部性”向“全局性”迈进，便成为了算法交流后教学引导的主要视点。我们看到，汪老师留给了学生充足的思考空间，让其结合实际问题来阐明“中括号”的使用缘由和运算原理，再通过对计算过程的质疑、争辩，进一步强化了“脱式计算”的格式步骤与注意事项。尽管，这里看不到“新授”的痕迹，但解决问题策略交流的充分互动和随机点拨，使得“中括号”已深层纳入全体学生的认知视野。
　　片断三：互动评价，强化“中括号”的应用规则
　　师：刚才，列综合算式解决问题时，我们用到了一个数学符号——“中括号”。现在，你们能再用综合算式来解答“5个这样的网球要多少钱”这个问题吗?
　　(学生独立解决，教师搜集有代表性的解法，并板书于黑板上)
　　①(300-60)÷12×5?摇?摇 ?摇②［(300-60)÷12］×5
　　③5×［(300-60)÷12］?摇?摇?摇④5×(300-60)÷12
　　师：你对这几种方法有没有什么想说的?
　　生1：我认为第④种方法是错的，(300-60)÷12要加上中括号。
　　师：为什么要加上中括号呢?
　　生1：不加中括号的话，第二步要算5×240了，意思讲不通。
　　师：而我们要算的是240÷12，也就是网球的单价，所以要加上中括号。
　　生2：第②种方法的中括号多加了。
　　师：怎么讲?
　　生2：因为第二步本来就是先算除法再算乘法的，中括号加跟不加一样。
　　师：有道理!刚才，谁是用第②种方法解答的?(一生示意)你刚才为什么要加中括号呢?

[1] [2]  下一页